Kecerdasan Buatan Hukum Ketidakpastian
Selamat Datang di Blog Orang IT. Didalam ilmu komputer tidak selalu yang pasti-pasti tetapi ada juga yang tidak pasti. Banyak masalah didunia ini yang tidak bisa dimodelkan secara lengkap dan konsisten, contohnya penalaran induktif misalnya ada sebuah premis:
premis 1 : aljabar adalah pelajaran sulit
premis 2 : geometri adalah pelajaran sulit
premis 3 : kalkulus adalah pelajaran sulit
konklusi/kesimpulan : matematika adalah pelajaran sulit
Banyak sekali yang mengatakan bahwa matematika merupakan pelajaran yang sulit tetapi menurut saya seperti bermain game atau coding (ilmu pasti). Seandainya matematika sulit maka tidak mungkin ada begitu banyak pakar matematika
Yang paling sulit adalah tentang pelajaran hidup hehe 👪
Ketika muncul sebuah premis baru hal itu dapat mengubah hasil kesimpulan, misalnya kita tambah;
premis 4 : biologi adalah pelajaran sulit
lalu bagaimana konklusi nya?
"Matematika dan IPA adalah pelajaran yang sulit"
Jadi ketika kita membicarakan masalah ketidakpastian sebenarnya ilmu yang digunakan sudah pasti, tetapi ketika muncul premis baru misalnya kita buat aplikasi sistem pakar pendeteksi penyakit bawang merah
Baca juga: Sejarah AI (Artificial Intellgence)
Penyakit bawang merah ada 5 jenis, di tangkai , batang dsb seiring perkembangan teknologi muncul jenis penyakit baru dan menambahkan premis maka kesimpulannya juga akan berubah
Ketika kita membicarakan masalah ketidak pastian maka berhubungan dengan penalaran. Ada 2 jenis penalaran;
1. Penalaran non monotonis
Suatu penalaran dimana fakta baru mengakibatkan ketidak konsistenan, ciri-ciri;
- mengandung ketidak pastian
- adanya perubahan pada pengetahuan
- adanya penambahan fakta baru yang merubah konklusi (dibutuhkan penalaran statistik)
Ketika dokter memberikan resep gejala penyakit hipertensi, berapa besar persentase keyakinan dan ketidak yakinan dokter mengenai hasil analisis? bisa kita hitung menggunakan hukum ketidakpastian
2. Penalaran Monotonis
Ciri-cirinya bersifat konsisten dan pengetahuannya lengkap
Contoh: Pembuatan project pada sistem pakar kerusakan televisi tabung, ketika kita membicarakan sistem pakar televisi tabung maka datanya ada cukup banyak, ada seorang pakar dan buku pengetahuan.
Misal televisi tabung warnanya merah dan ini disebabkan oleh kerusakan elektron gun (elektron-elektron yang bertugas menyalurkan sinar/panas agar bisa memancarkan fosfor didalam tabung sehingga membentuk warna dimana elektron warna terdiri dari 3 jenis yaitu R, G dan B dimana ketiganya harus bergandengan. Ketika elektron gun rusak maka fosfor yang ada didalam televisi tabung berpencar/tidak konsisten sehingga layar televisi berwarna merah
Contoh lain pada sistem pakar kerusakan handphone xiaomi, mesin cuci, ketika mesin cuci rusak didalam buku manual panduan sudah dijelaskan masalah error dan solusinya (konsisten/pasti)
Pesan E1 (error 1) mungkin menandakan adanya komponen yang tidak bisa berputar, lalu E2 airnya tidak mau keluar dan itu tidak pernah berubah. Jadi pembuatan sistem pakar tentang produk elektronik masuknya kedalam penalaran monotonis
Karena konsisten dan tidak akan pernah berubah (bersifat tetap)
Salah satu teori yang membahas tentang ketidakpastian salah satunya adalah probabilitas (kemungkinan)
Bentuk teorema bayes
P(Hi|E) = probabilitas hiposessis Hi, benar jika diberikan evedence E1
P(E|Hi) = probabilitas munculnya evicende E, jika diketahui hipotesis Hi benar
P(Hi) = probabilitas hipotessis Hi menurut hasil sebelumnya tanpa memadang evidence manapun
N = jumlah hipotesis yang mungkin
Misal, ada contoh kasus begini
Si Jokow mengalami gejala bintik-bintik diwajahnya. Dokter menduga bahwa ia terkena cacar dengan :
*bintik-bintik (gejala) sebagai evidence sementara cacar (penyakitnya) sebagai hipotesisnya
Probabilitas munculnya bintik-bintik diwajah, jika si jokow terkena cacar P(bintik2|cacar) = 0,8
Probabilitas si jokow terkena cacar tanpa memandang gejala apapun P(cacar)=0,4
Probabilitas munculnya bintik-bintik diwajah jika si jokow alergi P(bintik2|alergi)=0,3
Probabilitas si jokow terkena alergi tanpa memandang gejala apapun P(alergi)=0,7
Probabilitas munculnya bintik-bintik diwajah jokow jika itu adalah jerawat P(bintik2|jerawatan)= 0,9
Probabilitas si jokow terkena jerawatan tanpa memandang gejala apapun P(jerawatan)=0,5
Pertanyaan 1:
Berapa probabilitas si jokow terkena cacar karena bintik-bintik diwajahnya?
Kita cari dulu P hipotesis terhadap evidence P(Hi)
P(Hi) = cacar
P(E) = bintik2
Pertanyaan 2:
Berapa probabilitas si jokow terkena alergi karena bintik2 diwajahnya?
P(hi) = alergi
P(E) = bintik2
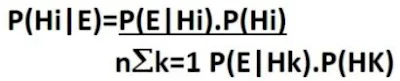



Posting Komentar untuk "Kecerdasan Buatan Hukum Ketidakpastian"
Posting Komentar
Artikel di blog ini bersumber dari pengalaman pribadi penulis, tulisan orang lain sebagai posting tamu maupun bayaran oleh sebab itu segala hak cipta baik kutipan dan gambar milik setiap orang yang merasa memilikinya